晚上10点多，累了一天的我刚刚睡着，就被一阵刺耳的电话铃声吵醒。

我刚按下接听键，那头便传来一个孩子欣喜而急切的声音：“老师，我的想法是对的！今天中午和晚上我实验了很多遍，我的想法是对的！”我还没明白是怎么回事，只听那孩子接着讲道：“今天我们学习的环形面积，可以采用剪拼的方法，把环形转化成平行四边形，利用平行四边形的面积计算方法求出环形的面积……”

打电话的孩子是我的一位学生，他的话把我的思绪带回了今天上午的数学课堂。

上午的第二节是数学课，学习“环形的面积”。这节课难度不大，通过一番交流、演示、论证之后，孩子们都露出了满意的笑容，收获满满。正当我为这一节课的成功和高效沾沾自喜时，一位成绩平平的男孩子高高地举起了小手，只听他说道：“我觉得两个同心圆组成环形的面积，也可以像圆面积的推导方法一样，把环形进行剪拼，然后拼成一个平行四边形，再用平行四边形的面积计算方法求出环形的面积。”这种方法超出了我的预设。

马上就要下课了，剩下的时间肯定不够再和他纠缠这个问题……各种因素促使我必须中断和他的进一步交流。班里不知哪个同学又不耐烦地冒出了一句：“用大圆面积减去小圆面积多简单呀，干嘛又剪又拼的那么麻烦？”

“是啊！”“就是！”大家你一言我一语地附和道。

这个孩子的表情变得紧张起来，我也感受到了自己的失态，赶忙想了一个折中的办法：“那样吧，这只是你的猜想，你想办法证明一下，明天上课展示给大家好吗？”下课铃声响了，在孩子们的“老师再见”声中我走出了教室。进而在接下来的忙碌中将这件事抛在了脑后，没想到……

第二天一上课，我就请那个孩子进行展示。

从他熟练的操作可以看出，为了证明自己，他之前进行了多次的实验和操作。只见他把环形纸片剪成偶数等份，每一份都是一个小扇环，看作近似的梯形，然后进行拼接，转化成了一个近似的平行四边形（如图1）。这时，孩子还不忘补充道：“根据极限思想，平均分成的份数数越多，拼成的图形越接近长方形。长方形的长相当于环形的‘外圆周长÷2+内圆周长÷2’，长方形的宽相当于环形的环宽，长方形的面积=长×宽。所以：环形的面积=（外圆周长÷2+内圆周长÷2）×环宽。”（如图2）

我和同学们被他精彩的讲解深深地吸引。

我激动地说：“此处应该有掌声！”我动情地给大家讲述了这个孩子的探索的历程——“我觉得，这掌声是对他不服输的精神的肯定，更是对他积极的探索精神的鼓励！”

更加精彩的一幕顺势呈现。

“同学们，根据刚才的探索结果，环形的面积=（外圆周长÷2+内圆周长÷2）×环宽，如果把这个公式进行变形，你还能有什么新的发现？”在我的启发下，孩子们有的疾笔演算，有的小声交流。只听一个孩子喊道：“老师，我发现环形的面积=（外圆周长+内圆周长）÷2×环宽，也就是通过两个圆的周长和环宽也能求环形的面积。”

“我们也是这样想的！”孩子们显然表现得比较激动了。

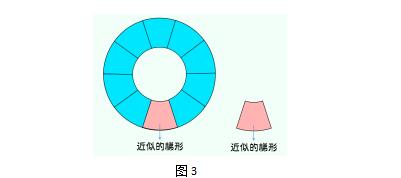
我觉得时机已经成熟，就神秘地说：“你们太了不起了。结合你们的发现，看屏幕演示（如图3），这个扇环可以看作近似的什么图形（梯形）？”

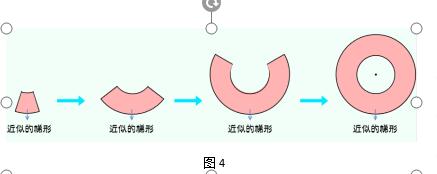
我通过课件演示，扇环的两条弧逐渐变长，直到变成一个环形（如图4）。“还是扇环吗？这个环形还可以看成一个近似的什么图形？这个环形与这个近似图形又有什么联系呢?”

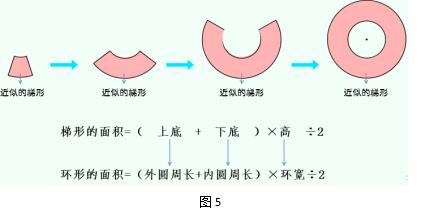
在我的一系列演示、启发和追问之下，课堂气氛达到了高潮，孩子们争先恐后地回答：“环形还可以看作是一个梯形，环形的内圆周长就是梯形的上底，外圆周长就是梯形的下底，环宽就是梯形的高，梯形的面积=（上底+下底）×高÷2，所以环形的面积=（外圆周长+内圆周长）×环宽÷2。”“孩子们，老师为你们的精彩表现点赞，对比刚才通过剪拼得到的环形面积公式，它们居然不谋而合，互相验证了两种方法的正确性！”（如图5）

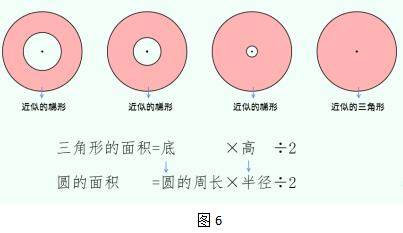
“让我们的思维飞得更高一些，我们的视野将会更开阔。”我一边说，一边用课件演示，将环形的内圆逐渐缩小，直到变成一个点（如图6）。

“你看到了什么？”学生齐声回答“圆”，声音还没落，就有孩子说：“圆还可以看作一个上底为0的梯形。”“上底为0的梯形不就是一个三角形？圆还可以看作是一个三角形，三角形的底是圆的周长，高是圆的半径，三角形的面积=底×高÷2，所以圆的面积=圆的周长×半径÷2。”

“哇塞，太神奇了！”

“老师，我们学习圆面积的推导公式时，其中有一步是‘圆的面积=圆的周长的一半×半径’，刚才的‘圆的面积=圆的周长×半径÷2’和这个不是一样的吗？”我肯定道：“对，两种方法的又一次互相验证。”

激烈地争辩让我感到课堂一度失控，这种失控让我和孩子们一起在思辨、验证和发现的世界里尽情地翱翔……